Day 45

Presentation

This morning Jordan, Peter and I presented our work to a group of AHS electricians and Janet. We got some valuable feedback about how we can best serve their needs.

I was pleased to hear that somewhere out there is occupancy information for the thermostats, which I could tap into and use as a replacement for my current holiday/half-day variables.

Putting the model to use

I’ve gotten the model to a point that I think it could be useful. I want to shift from the static sample file that I’ve used all summer to using the most up-to-date data so I can start making real predictions. I’ve asked Anil for help on this, as I don’t know where all of the updated data is stored.

That’s the next big focus for me. In the meantime I can play around a bit more with the sample data (maybe try it out on Bancroft). I can also start laying the groundwork for the prediction database.

More intuitive window

Currently the 15-minute time interval is hardcoded into the application (I specify 4 points per hour, i.e. 96 per day). This may not always be the case for certain meters or datasets. I can generalize the points-per-day calculations with:

data_freq = '15 min'
pp_day = int(pd.Timedelta('1 day') / pd.Timedelta(data_freq))

I would also use data_freq to resample the data at the start and if needed cut off incomplete days.

Then I can incorporate pp_day into my window calculations:

input_size   = pp_day*7*4
gap_size     = pp_day
output_size  = pp_day

That way if the situation requires a different frequency of data points I only need to change data_freq (which is an easily understood string).

Do I need a testing set?

In a realtime context I’m not sure how to handle model validation. If I continue doing things the way I have so far (splitting the data into a training/test set) then the most recent data will be used for testing rather than training. That means if there is a recent change in power usage which would have a significant impact on predictions, the model would be delayed at learning it.

I think that for RF, validation isn’t as important since it already reduces variance as an ensemble of random decision trees. I might just ditch it altogether, which leads to my next difficulty…

Rethinking the threshold

Without a testing set I can’t estimate the RMSE of the predictions, which is how I was setting my threshold. I’m not sure if this is the best approach for setting the acceptable regions for power values.

I googled “random forest standard deviation” and found this page that talks about prediction intervals. What’s different about this approach is that it doesn’t require that you know the true values ahead of time, it just uses information about discrepancies between the predictions of each of the forest’s trees.

I quickly tried implementing it and had some trouble, because it appears to only work for single dimensional output.

Tweaking the implementation

It wasn’t too hard to fix, I pretty much just had to specify the axis of the percentile calculation:

def pred_ints(model, X, percentile=95):
    err_down = []
    err_up = []
    for x in range(len(X)):
        preds = []
        for pred in model.estimators_:
            preds.append(pred.predict([X[x]])[0])
        err_down.append(np.percentile(preds, (100 - percentile) / 2. , axis=0 ))
        err_up.append(np.percentile(preds, 100 - (100 - percentile) / 2. , axis=0))
    return np.array(err_down), np.array(err_up)

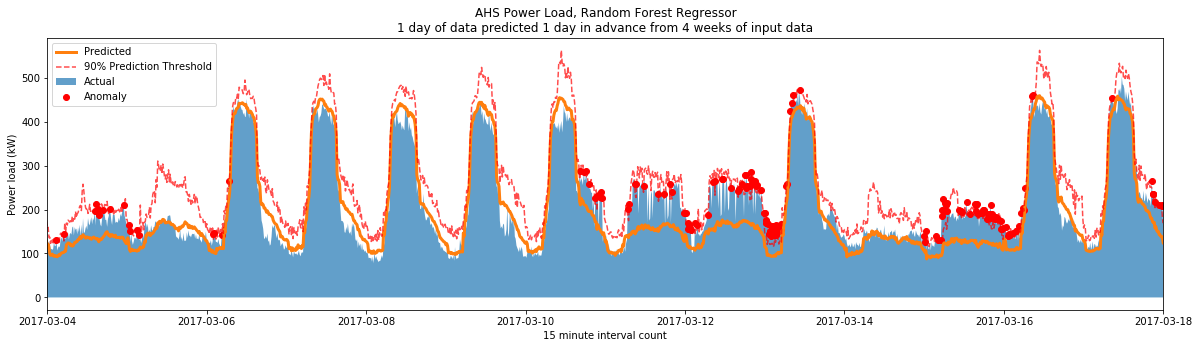
This calculates a unique prediction interval for every data point (not just for each day) based off the inner $X\%$ of the sub-trees’ predictions.

Here’s how it changed the plot:

You can see that now the threshold is dynamic across time. In some cases it’s more forgiving of the actual values, such as ³⁄₁₁-³⁄₁₂. This more fairly accounts for areas where the model is unsure of its results as opposed to setting a constant threshold height.

I still want to look at other sources and do more research before I fully commit to this threshold approach.