Day 40

To follow up on a note I made yesterday about the research paper Early-warning application for real-time detection of energy consumption anomalies in buildings, I found another paper published by some of the same authors that goes deeper into the techniques they used.

Here is another paper that reviews a variety of forecasting techniques for time series data. It’s actually incredibly detailed and includes topics like moving averages (similar to the rolling medians I tried early on), SVMs, ARIMA, Artificial Neural Networks, and many more. It lays out the pros and cons of each. It also explains the benefits of using all sorts of hybrid methods.

Here’s a quote from it that stood out to me regarding the use of temperature data in another study:

It was seen that the treatment of the dataset as pure time series data gave better results rather than considering other factors like ambient temperature to predict the load demand.

Additionally, here is a whole online book about the process of forecasting data values. It will be a valuable resource no doubt.

Lag features

Currently I’ve been using regression techniques that rely on variables extracted from a single point in time. I ask the model, “How much power will I use on the first Tuesday in January at 9:00am when it’s 30 degrees outside?“, and it returns a value.

However, another approach is to use a window of previous values as the inputs. These are referred to as lag values. You’d ask, “How much power will I use next given that I just used these values recently?”. One benefit here is that it doesn’t require as much data to learn how to make predictions, whereas my previous method would need data across a wide range of scenarios (albeit making a more accurate model).

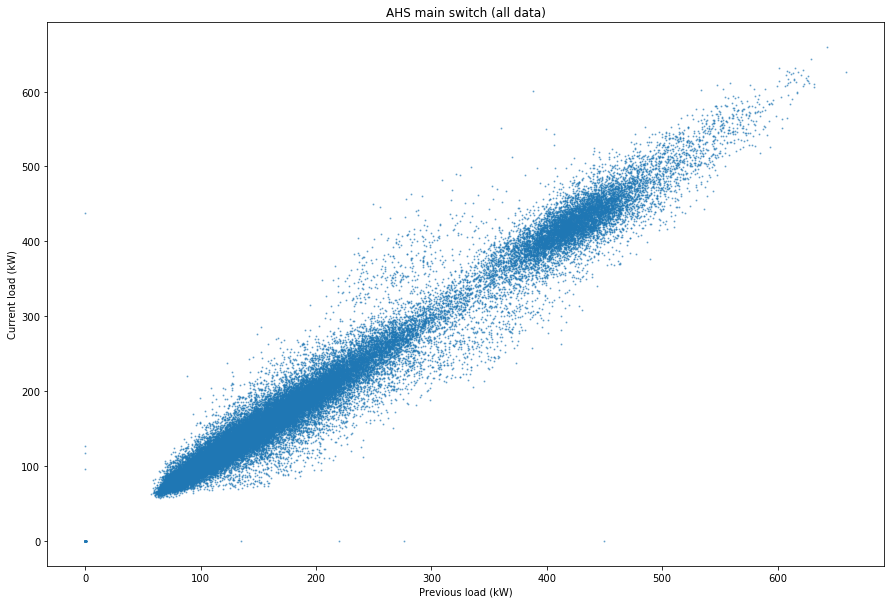
As a really naive example, here’s a plot showing the autocorrelated nature of the timeseries data, comparing each power usage value to the one that came before it (this obviously can’t be used for prediction):

I could even combine lag features with features about the current time.

My main stumbling block is deciding which approach to take. Should I keep looking at this as a regression problem with a broader range of features? Should I try a timeseries approach like S/ARIMA/X? Should I look into neural networks? This response suggests that all are valid options.

EDIT: I just realized that the method I used in the next section isn’t really valid for forecasting since it used the lagged actual values in the testing inputs. Instead I think I’d have to iteratively predict values and use those predictive values as lagged inputs for future points.

Amazing results

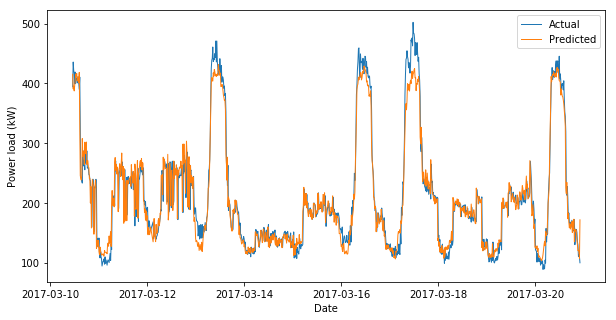
I’m a little scared by how good these results are… I tried adding some lag features into an SVR and got great scores (over 90% $R^2$). I will do a better implementation next time but I’m already blown away by what I’m seeing. I trained on 4000 data points and tested on the following 1000. Here’s what I got:

Wow. That looks pretty darn good to me. Before I get too excited I should remember that a perfect fit is not always a good thing. But I like the fact that the prediction is a little under the actual, leaving area for improvement.

Dummy variables

I was under the impression that I could just represent variables like day of the week, month of the year, etc., with quantitative values (e.g. 0=Jan, 1=Feb … ). However, most of the resources I see instead say to use $n-1$ dummy variables for the $n$ options. I don’t totally understand why since the intervals are meaningful (the difference between day 1 and day 2 of the week is 24hrs just like between days 4 and 5) but I’ll roll with it.

To do

I whipped up the lag feature implementation pretty quickly, but next time I’ll need to do a lot more extensive testing and maybe use some more proper cross validation. But this was a very good way to end the day.

EDIT: I need to rethink the implementation of lag features.