Day 36

Normalization strikes again

I thought I had found the solution yesterday to my normalization problem since the plot looked much better. Today I tried running the whole plot (with the residuals and everything) where I saw my first red flag - the residuals were not displaying properly. After some time debugging, I noticed that my regression’s predict function was returning different values for the same inputs depending on how many samples you passed in - not good!

When using the normalize parameter this behavior does not occur. It makes sense why the issue is happening right now - I’m normalizing along the columns so as I add more columns (one for each input) the will all have to scale down accordingly. As to why I didn’t notice this before, it’s likely because I plot my regression line as 100 uniform samples, which is close to the 114 samples I used to create the model.

To get to the bottom of this I went to the scikit-learn source code and started a scavenger hunt for how the normalize parameter is implemented. It led me to this _preprocess_data function in the parent linear_model class. Maybe I could manually call this function to perform the appropriate normalization procedure for the Huber regression?

I copied the Ridge regression’s call to _preprocess_data:

self._preprocess_data(
            X, y, self.fit_intercept, self.normalize, self.copy_X,
    sample_weight=sample_weight)

Then I replaced the references to self with the variable for my Ridge object and X and y with my actual data variables, and it spat out some tuples so I hope it worked. I then tried the same process with a Huber estimator, and at first it gave an error because the estimator has no copy_X attribute. So for the attributes that don’t exist for Huber estimators I went to the Ridge documentation and replaced them with Ridge’s default values (since I just want to replicate Ridge’s behavior). The Ridge default is True which matches the _preprocess_data default, so I can actually just delete that argument altogether. Finally I forced normalize=True. It successfully returned the same tuple as the Ridge object did. Remember that this is just a preprocessing step, so there’s no reason for the two estimators to return different values yet.

The items it is returning are X, y, X_offset, y_offset, and X_scale. Unfortunately the Huber estimator doesn’t use those parameters, so I’d have to somehow implement the manually. This seems like far too complex of a solution for what should be a simple problem. I’ve posted a help thread on a stats forum for a recommended solution so I don’t waste time trying to solve this on my own.

The real solution(?)

I’m hestitant now to claim to have the “solution”, but I got a response to my post that seems to mostly fix my issue. It comes down to how you define normalization. In some contexts it means the scaling a vector to unit length (as the Normalizer() object and normalize() methods do), but in this case it’s referring to scaling values to have unit variance and mean of zero.

Therefore I should be putting StandardScaler() in my pipeline rather than Normalizer(). It doesn’t completely replicate the output of the normalize parameter but it’s pretty close and can be adjusted by the estimator’s parameters.

Now I get consistent predictions regardless of how many items I predict on.

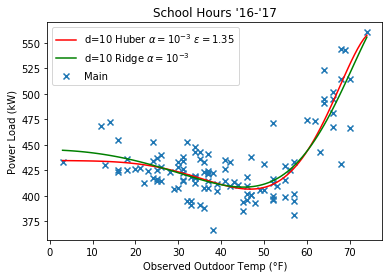
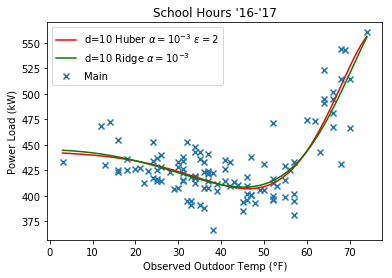
Here’s some plots comparing the Huber regression to Ridge, note that they look more similar at a higher $\epsilon$ value.

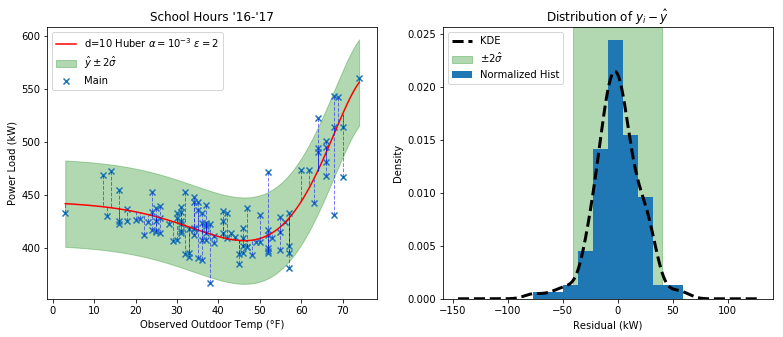
And here’s how the residual distribution looks:

It may look similar to the Ridge plot, but if you throw in some outliers you’ll quickly see the difference.

Robust Scalers

As another followup to my post, I learned that there is a RobustScaler that as the name implies, uses a more robust method for scaling based of interquartile ranges. I also could potentially make my own scaler using the scaled MAD as a unit of variance. From my brief testing, these would take some debugging to implement properly (so far they make the fit worse).

To do

Tomorrow I will be catching up with Anil at the library. I’ve made decent progress with picking an estimator, next on my agenda is to focus on cross validation.