Blog update - site search

As my blog has grown, it’s gotten harder to find specific posts from the archive. This weekend I had some free time on my hands so I got to implement client-side search on the site. I’m using Hugo’s output configuration parameter and an index.json template to create a search index of my posts. Lunr.js performs the necessary search algorithms in my search script. The result is a lighting-quick site search that doesn’t need to even reload the page - try it out on the home page. It was a neat learning experience.

Improving the estimator

Quick note on pipelines

Previously I would manually run the PolynomialFeatures fit_transform() on my sample points prior to fitting and on my test points prior to prediction. sklearn.pipeline streamlines this process by letting me build the PolynomialFeatures tranformations straight into my estimator.

Example:

model = make_pipeline(PolynomialFeatures(degree=5), linear_model.LinearRegression())

To get the coefficients of the underlying estimator, you would call model.steps[1][1] or model.named_steps[<name>] and access the coef_ attribute.

Ridge regression

Ridge regression is a step up from the basic LinearRegression object. Its cost function includes a regularization term consisting of the l2-norm of the parameter vector scaled by a constant $\alpha$.

The default arguments do practically nothing for me, probably because the size of the squared error term vastly outweighs the regularization term for this data. It think as the number of samples grows, the squared error term grows (since the l2-norm is inherently summing more things) but the regularization term can potentially stay constant (since the parameters don’t necessarily change, and the number of parameters is constant)

To get around this, I found it useful to set normalize=True, which resolves the scaling issue between the penalty factor and the size of your sample.

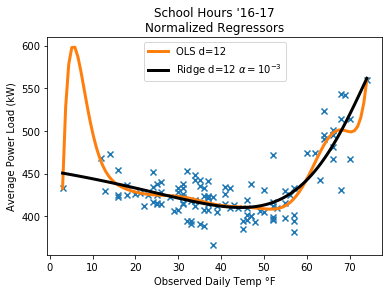
Here you can see how the ridge regression does not suffer from the same overfitting problem as the basic least squares regression, even when permited to use 12th polynomial features. Since the regressors are normalized, $\alpha$ can be quite small (otherwise I had to set it to around 10,000 to achieve similar results)

Energize module update

Every day I’ve been copying and pasting the same variable definitions into my code. I finally got around to actually moving these definitions into the energize module since I always end up referencing variables like df_energy or df_school. Now they’re defined once and I can access them from the energize prefix.

Additionally, I added a function that finds the intersection of two Pandas objects by thier indexes (strange that there isn’t one built into Pandas) called intersect().

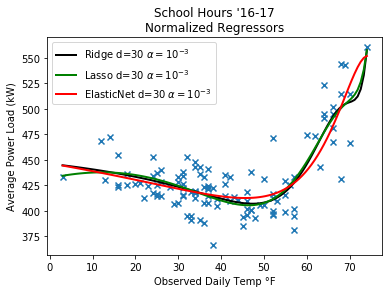
Lasso and ElasticNet

Lasso is quite similar to Ridge regression, but it differs in the implementation of the penalty term. While Ridge has the goal of reducing parameter sizes, Lasso has the goal of reducing unecessary parameters. There’s also a method Elastic Net which combines the two (it has an l1-norm and l2-norm penalty term). By default it uses a ⁵⁰⁄₅₀ ratio between the two.

I spent some time tweaking the degree and $\alpha$ levels. Overall, I found that the Ridge & Lasso regressions were more closely fitted than the ElasticNet, but most of the differences I was seeing could be settled by simply adjusting the $\alpha$ value. There’s not a clear winner for me yet.

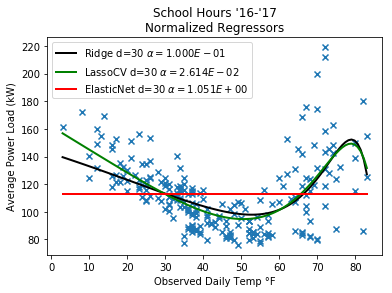
Cross validated estimators?

I tried out the cross-validated versions of these estimators out without much luck. I’ve been mainly sticking with the default values they provide though, so perhaps that is part of the problem.

I’m using the alpha_ attribute to get the cross validated alpha values. They seem to be performing worse on their own than when I manually specified the alpha value. I’ll have to spend more time reading about how they’re supposed to be implemented, but so far changing the cv, max_iter and tol arguments hasn’t provided a clear benefit.

To do:

I want to look into robust regression estimators and figure out what’s going wrong with the cross validation. I also should find out whether the standard error of the residuals can be used as a way to detect trend outliers.