Day 29

Today I’ll be taking a look at the new Bancroft school data. Bancroft is supposed to be a very energy efficient building so it’ll be ineresting to compare the energy usage patterns to AHS.

The simplest filter to compare would be night data. Some activities may go on during the summer or weekends, but most buildings will not be operating at night.

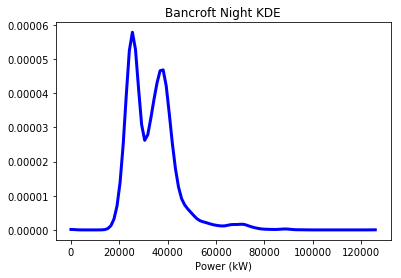
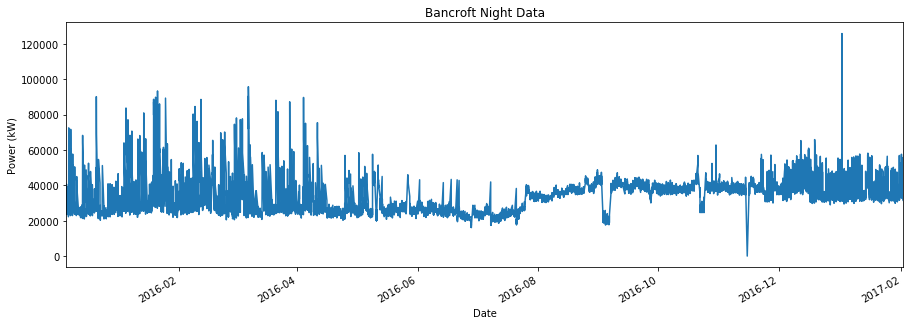
Interestingly we’re seeing a bimodal shape in the night-time distribution. To see why I can look at the line plot:

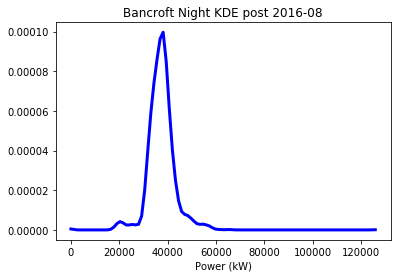
The baseline usage starts out a bit above 20,000 kW, then after August 2016 it rises to around 40,000 kW. Filtering just the data points that are after this point in time yields a more familiar shape:

Catching Errors in the Time Filterer

When I tried running the school filter on the Bancroft data, I noticed an issue with the time filtering method. When you specify bounds that extend past the range of the data, usually it extends as far as it can and doesn’t raise an issue. But when specific dates are out of the data range, it throws a KeyError. To combat this, I added a Try/Except block in the data range token parser:

if (type(token)==str):
    try:
        return data[token]
    except KeyError: #returns None
        print('[!] energize.py : range_token_df : ' + token+' not in range')

This way it lightly warns you about your unused dates without causing the script to halt. Strangely, by default Pandas won’t throw a KeyError if you use slice indexes that are completely out of the data range (it’ll just return an empty data set), it only does the error for individual bad indexes.

Nonlinear Regression

I spent a lot of time today fumbling around web pages describing various regression techniques. Viraj elaborated on the Poisson regression that I probably could consider the decimal kilowatts used as “counts” of infinitesimally small wattage units, and he shared my concern about the independence of the events. This example from Wikipedia is somewhat reassuring that the events could be considered independent (since counts are wattage units used, and using a unit of power does not make it more or less likely to subsequently use another unit of power).

However, Viraj also noted that Poisson regression is just one of many regression techniques available, which led me down the rabbit hole of online resources on the subject.

I ended up finding something very promising on the topic of non-linear regression. This Carnegie Mellon lecture goes over exactly what I hope to achieve, fitting a non linear multi-dimensional model to a data set. The professor literally uses power data compared against variables like temperature and time of day. It’s almost funny how perfect of an example this is. It’s comforting to see the familiar tilted-U shape in the lecture’s temperature versus power plot as I saw in Day 12. The video is quite long and I’ve only seen part of it, but tomorrow I will try to cover as much as seems necessary and probably look at other sources.