Day 10

The pandas rolling object has a few built in commands that I have already made use of, like .median(). But for broader scenarios, you can use the .apply() function to, as the name suggests, apply your own function across the windows.

The function must accept a Numpy array (I wish it was just a Series instead) and return a single number. For the time being I made a temporary function to handle Numpy median absolute deviations.

def np_mad(nda):
    ser = pd.Series(nda)
    return abs(ser-ser.median()).median()

I’m more familiar with Pandas than Numpy so for convenience I simply converted the input Numpy array into a Pandas series, then performed the usual MAD calculation on it. If I become more comfortable with Numpy I can change the function but for now Pandas is my easiest option for item-wise calculations.

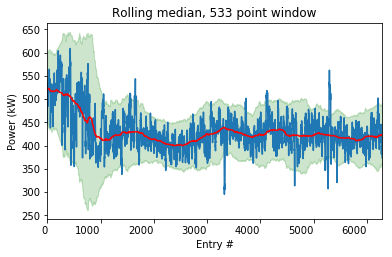
I then used Matplotlib’s .fill_between() feature to highlight the regions above and below the rolling median. I will set the bounds as $median \pm 2.5\hat{\sigma}$. The result looks like this:

The shaded region encloses values deemed acceptable. The points where the power plot moves past the shaded bounds signify problem areas.

Compared to the basic horizontal line I started with last time, this is a much more dynamic indicator of abnormality because the acceptable region changes is value and range according to the trend and volatility of that time period.

Variables

The qualification for abnormality is determined by a couple of factors that are not set in stone. First is the window size. I explained yesterday my reasoning for selecting 533, but if you are looking at a shorter sample you would want a smaller window. The smaller your window, the more your medians and MADs are affected by sudden changes.

There’s also the factors that I am applying to the MADs. I’m pretty sure the normal scaling factor is good to keep, but I’m not set on the 2.5 value. Perhaps 2 or 3 would be better. I played around with this value on my own and found 2.5 to be a happy medium that didn’t flag too many points but didn’t ignore too many.

One thing to consider would be getting rid of this variable altogether. Instead of specifying a threshold value, we could calculate the ratio of each value’s distance from the median over the MAD, and rank them from most abnormal to least abnormal. That would let the adminstrator simply take care of the worst offendors as they please.

Abstracting it

Given a Series of power usage with datetime indexes and a window size, I want to be returned a Series with datetime indexes of the ratio $\frac{e_{med}}{MAD}$ where $e_{med}$ represents the residual (deviation) from the median.

I thought this was going to be an annoying process, because when plotting I had to keep stripping indexes and performing data interpolation to avoid errors. But I didn’t have to do any of that. Note that I am storing my generic functions in an energize.py module which I am importanting as egz. My sample calculations and plots are performed in a seperate temporary script.

def mad(series):
    return abs(series-series.median()).median()

""" mad_rankings: Series, int --> Series
Returns Series with ratios of median residual / MAD
uses rolling window of desired size (data point count)
"""
def mad_rankings(series, w_size):
    roll = series.rolling(window=w_size, center=True, min_periods=1)
    meds = roll.median()
    # convert numpy nd-array into pandas series before calculation
    mads = roll.apply(lambda nda: mad(pd.Series(nda)))
    return (series-meds)/mads

Now if I say

school_main[egz.mad_rankings(school_main, 533)/1.4826 > 2.5]

I am handed a series of main power usage entries while school is in session that are more than 2.5 estimated population standard deviations from the month-wide median trend. Isn’t that a mouthful!

A more intuitive window

I don’t think my current window implementation is ideal because data point count is not user-friendly. Also, jumping over gaps disrupts seasonal shift scale (e.g. the ‘month’ that includes winter break spans more than a month of actual time)

I should at least try switching to a strictly time-based approach and see how disjointed the result looks.

It’s not as simple as just changing the window argument to one of the predefined pandas offset string values. If I say window='M' I get the error:

ValueError: <MonthEnd> is a non-fixed frequency

Pandas doesn’t like the fact that not all months contain the same amount of data. From what I’ve found online, the easiest way to remedy this is to resample the data at a fixed frequency. All of the entries that don’t have any actual data will be marked null or Nan. To make this more complicated, the sample data isn’t really taken at a fixed frequency. A majority of it is at 15 minute intervals, but I see some values at odd times. I don’t know how inefficient this would be, but perhaps I could resample at a high detail, like every minute.

I tried this with school_main.reindex(pd.date_range(school_main.index.min(),school_main.index.max(),freq='1min')) but still got the same non-fixed frequency error.

Oddly enough when I use days instead of months, I don’t get an error. I assumed the error was because some months are longer than others, but every week is the same duration of time. Oh well. I will just stick with days for now. I can simulate a month by just saying 30 days.

Note: time index based rolling windows don’t let you use the center feature.

Once I change to a time-based window I will have to redo my plotting code, since it is all based on count rather than time index. Here’s the new plot:

You can see the gaps where the plot line jumps suddenly. Those are the gaps in the data. Unfortunately there’s no easy way to hide those interpolated lines. Pandas will only show a gap if there’s a value marked Nan there. If my data were at a constant requency, I could resample and all the areas with gaps would default to Nan, but since the data is recorded at varying rates I can’t do this.

This definitely doesn’t look as pretty as the last chart, but the data it represents is a little more useful. It doesn’t seem to wrap around the power plot quite as nicely because of the lack of a center option. I’m going to have to revise my ranking function to take this into account too. More tomorrow.